در ریاضی سری عبارت است از مجموع جملات یک
دنباله.به عبارت دیگر سری شماری از اعداد است که بین آنها عملگر جمع قرار گرفته است.
سریها بر دو نوعند:سریهای متناهی و نامتناهی؛که سریهای متناهی را می توان با اعمال ساده جبری محاسبه کرد،ولی برای محاسبه سریهای نامتناهی باید از آنالیز کمک گرفت.
به عنوان مثال سری زیر یک سری متناهی است.
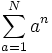
سری نامتناهی، سری میباشد که جملات آن محدود نیست.
به این سری توجه نمایید:

این سری یک سری عددی نامتناهی میباشد.که در حالت کلی به صورت زیر نشان داده میشود.که به آن
سری هندسی میگویند.
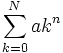
a را جمله اول و k را قدر نسبت سری می نامند.مجموع n جمله اول یک سری رابا
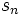
نشان میدهند
در صورتی که
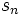
به سمت یک عدد متناهی سیر کند آن را همگرا مینامند. در غیر این صورت به آن یک سری واگرا گویند.
حال به معرفی نوع دیگری از سریها به نام سریهای توانی می پردازیم:سریهایی را که جملات آن توابعی از متغیر x باشند را سریهای توانی گویند.و مجموعه مقادیر از x که به ازای آنها توابع موجود در سری تعریف شده و سری همگرا باشد را
میدان همگرایی سری گویند.
هر سری تابعی به شکل

را یک سری توانی بر حسب
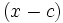
میگویند.واضح است که جملات آن به فرم زیردر میآید:
حال به قضیه مهمی به نام قضیه
تیلور میرسیم؛طبق این قضیه میتوان هر تابعی را که در یک بازه بینهایت بار مشتق پذیر باشد میتوان در این بازه به صورت یک سری توانی نامتناهی که به سری تیلور معروف است نشان داد.به عنوان مثال تابعی مانند

را میتوان به صورت جمع توابعی بر حسب

نوشت.
قبل از اینکه به توضیح کامل درباره این سریها بپردازیم.مثالی را در مورد این سریها بیان میکنیم.تابع sinx را در نظر بگیرید.این تابع را میتوان به صورت سری زیر بیان کرد:
لازم به توضیح است که در سری فوق c=0 در نظر گرفته شده است.
در اشکال زیر نمودار سری به ازای n=4؛ n=7 و نمودار sinx از راست به چپ رسم شده است.
همانطور که مشاهده میشود هر قدر تعداد جملات سری افزایش یابد شکل آن به یک منحنی تبدیل مشود.و اگر تا بینهایت رسم شکل ادامه یابد به شکل تابع sinدر مآید.
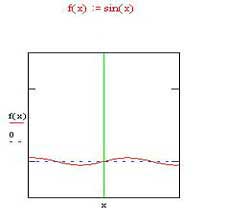
حال به شکل تابع sinx توجه کنید متوجه میشوید که با ادامه روند رسم اشکال به ازای nهای نامتناهی سرانجام به شکل sinx خواهیم رسید.
حال در زیر به تشریح کامل سریهای تیلور می پردازیم.
بحث جامع
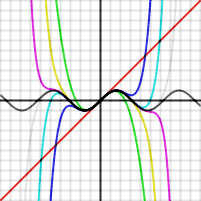
''
sin(x) و تخمین تیلور(Taylor)، چند جملهای های از درجه 1، 3، 5، 7، 9، 11 و 13.''
در ریاضیات،
سریهای تیلور از یک تابع
f حقیقی (یا مختلط) که معمولا بطور نامحدود
مشتق پذیر بوده و در یک
فاصله باز (
a-
r و
a+
r ) تعریف شده، بصورت
سریهای توانی زیر میباشد:
:

که در آن !
n فاکتوریل
n و (
f (n)(
a به معنی مشتق
nام
f در نقطه
a میباشد.
اگر این سریها برای هر مقدار
x در فاصله (
a-
r,
a+
r) همگرا بوده و مجموع آن برابر (
f(
x باشد، آنگاه تابع (
f(
x تحلیلی نامیده میشود. برای اطمینان از همگرایی سریها به (
f(
x، معمولا از تخمین برای جمله باقیمانده
قضیه تیلور استفاده میشود. یک تابع تحلیلی است، اگر و فقط اگر بتوان آنرا بصورت یک
سریهای توانی نمایش داد؛ ضرایب در سریهای توانی لزوما همان ضرایبی است که در فرمول سریهای تیلور داده شده است.
اگر
a = 0 باشد، این سریها به نام
سریهای مکلارین(Maclaurin) نامیده میشود.
اهمیت یک چنین سریهای توانی سه جانبه است. اول، مشتق گیری و انتگرال گیری سریهای توانی میتواند جمله به جمله انجام شود لذا بطور خاصی ساده است. دوم، یک تابع تحلیلی میتواند بطرز یکتایی به
تابع هولومورفیک(holomorphic) تعریف شده روی یک صفحه باز در روی
سطح مختلط، امتداد داده شود، که مکانیزم کامل
تحلیل مختلط را فراهم مینماید. سوم، سریهای (کوتاه شده) میتواند برای محاسبه مقادیر تقریبی تابع استفاده شود.
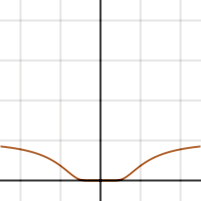
.
تابع e-1/x² تحلیلی نیست، مقدار سریهای تیلور 0 است، درحلیکه مقدار تابع غیر صفر است.
توجه داشته باشید که مثالهایی برای توابع (
f(
x که دارای مشتقات محدود بوده و سریهای تیلور آنها همگرا بوده ولی برابر (
f(
x نیست، وجود دارد. برای مثال، برای تابع تعریف شده مقطع بصورت (
f(
x) = exp(−1/
x² اگر
x ≠ 0 و
f(0) = 0،
تمام مشتفات در نقطه
x = 0 صفر میباشند، بنابراین سریهای تیلور (
f(
x صفر بوده، و شعاع همگرایی آن محدود است، اگر چه تابع بطور یقین صفر نمی باشد. این آسیب، توابع ارزشمند-
مختلط برای یک متغیر مختلط را مخدوش نمی نماید. توجه اینکه با نزدیک شدن
z به سمت 0 در طول محور فرضی (exp(−1/
z² به 0 نزدیک نمی شود.
بعضی از توابع را نمیتوان بصورت سریهای تیلور نوشت زیرا آنها دارای
حالت استثنایی می باشند؛ در این حالتها، اغلب نیز میتوان به بست سریهایی دست یافت اگر بتوان از توانهای منفی متغیر
x استفاده نمود؛ رجوع شود به
سریهای لارنت«Laurent). برای مثال، (
f(
x) = exp(−1/
x² را میتوان بر حسب سریهای لارنت نوشت.
قضیه پیشرفت اخیر برای یافتن سریهای تیلوری است که بتواند راهکاری برای معادلات دیفرانسیل باشد. این قضیه توسعه
تکرار پیکارد«Picard) میباشد.
فهرست سریهای تیلور
چندین بست سریهای تیلور مهم بشرح ذیل میباشد. تمام این بستها نیز برای متغیرهای مختلط
x صادق می باشد.
توابع اکسپتانسیلی و
لگاریتم طبیعی:
:

:
 سریهای هندسی
سریهای هندسی:
:
 قضیه فرعی-جزیی«Binomial»
قضیه فرعی-جزیی«Binomial» :
:
 توابع مثلثاتی
توابع مثلثاتی:
:

:

:

:

:

:
 توابع هایپربولیک
توابع هایپربولیک:
:

:

:

:

:

توابع لامبرت«Lambert's W):
:
اعداد Bk که در بستهای (tan(x و (tanh(x ظاهر می شوند همان اعداد برنولی ، (C(α,n در بستهای فرعی-جزیی ضرایب فرعی-جزیی بوده و Ek در بستهای (sec(x همان اعداد اولر می باشند.
چند بعدی
سریهای تیلور را به توابع با چند متغیر نیز تعمیم داد.
:
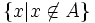
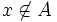 انگاه
انگاه 
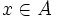 انگاه
انگاه 






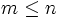 اگر و تنها اگر
اگر و تنها اگر 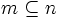 .
. 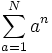

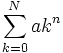
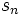 نشان میدهند
نشان میدهند 
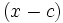 میگویند.واضح است که جملات آن به فرم زیردر میآید:
میگویند.واضح است که جملات آن به فرم زیردر میآید: 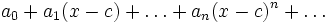
 را میتوان به صورت جمع توابعی بر حسب
را میتوان به صورت جمع توابعی بر حسب  نوشت.
نوشت. 




 .
. 

















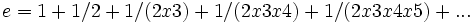

 نمایش میدهند. در هندسه اقلیدسی دو
نمایش میدهند. در هندسه اقلیدسی دو  محاسبه میکردند.(d قطر دایره در نظر گرفته میشد)که در نتیجه مقدار تقریبی عدد پی 3.1605 بدست میآید.
محاسبه میکردند.(d قطر دایره در نظر گرفته میشد)که در نتیجه مقدار تقریبی عدد پی 3.1605 بدست میآید. 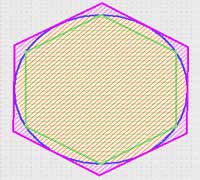

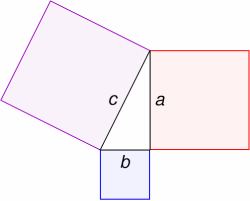
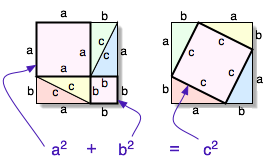
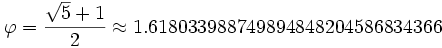
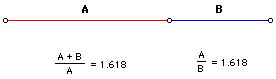
 را حل کنیم (کافی است بجای b عدد یک قرار دهیم بعد a را بدست آوریم) به نسبتی معادل تقریبا
را حل کنیم (کافی است بجای b عدد یک قرار دهیم بعد a را بدست آوریم) به نسبتی معادل تقریبا