هنریک آبل

آبل، ریاضیدان نروژی بود که در شهر فینوی متولد شد.در سال 1815، او وارد مدرسه کلیسای جامع کریستینا(اسلو امروزی) شد. سه سال بعد نشانه های نبوغ ریاضی در او ظاهر شد در همین زمان پدر او که یک کشیش فقیر بود، درگذشت و خانواده اش را در کمال فقر و بی چیزی، تنها گذاشت اما یک مقرری ناچیز که از پدر به جا مانده بود، اجازه می داد تا آبل وارد دانشگاه کریستینا شود.

اولین کار برجسته او اثبات امکان حل معادلات درجه پنجم بوسیله رادیکال بود. این تحقیق در سال 1824 برای اولین بار منتشر شد. و جزئیات بیشتری از آن در سال 1826 در مجله کرل منتشر گردید. او در سال 1825 به آلمان رفت و در حدود 6 ماه در برلین ماند. و در آنجا با آگوست کرل ریاضیدان آلمانی آشنا شد. او در همین موقع دست به انتشار مجله ریاضی زد، این کار آبل را دلگرم کرد تا دست به یک ریسک برای رسیدن به موفقیت بزند. بنابراین از برلین به فرایبورک رفت و در آنجا به پژوهش در مورد نظریه توابع جبری پرداخت.                                                          

                                                           
در سال 1826 به پاریس رفت و در طول اقامت ده ماهه اش، ریاضیدان برجسته فرانسوی را ملاقات کرد اما (استقبال آنها از کار و پژوهش او، بسیار ناچیز بود. فروتنی و تواضع او باعث شد تا او نتواند به طور گسترده تحقیقات خود را ارائه نماید و به علت بی پولی و نداشتن آزادی عمل نتوانست به موفقیتی دست یابد و سرانجام به نروژ بازگشت. در بازگشت به نروژ مقداری از وقت خود را صرف تدریس در دانشگاه کریستینا کرد. در آوریل 1829 پست استادی برای او در دانشگاه برلین پیشنهاد شد ولی نامه حاوی این مطلب 2 روز بعد از مرگ او به علت سل به مقصد رسید. او در موقع مرگ تنها 26 سال داشت.

آبل کارهای مهمی را در زمینه جبر انجام داد. آبل عهده دار توسعه های اساسی نظریه توابع جبری است و مهمترین کار او نیز همین بود. عبارت آبلین(مانند گروه آبلی در جبر) نیز از نام او گرفته شده است.

پی یردو فرما

زندگی

پیر فرما (Pierre de Fermat) در سال 1601 در نزدیکی مونتابن (Montauban) فرانسه متولد شد. او فرزند یک تاجر چرم بود و تحصیلات اولیه خود را در منزل گذراند. سپس برای احراز پست قضاوت به تحصیل حقوق پرداخت و بعد ها بعنوان مشاور در پارلمان محلی شهر تولوز (Toulouse) انتخاب شد.
او باوجود علاقه بسیاری که به ریاضیات داشت هرگز بصورت رسمی و حرفه ای به این علم نپرداخت اما با این حال بسیاری او را بزرگترین ریاضی دان قرن هفدهم می دانند. او در سن 64 سالگی در شهر کاستر (Caster) در گذشت.

قضیه ها

فرما برای تفریح به ریاضیات می پرداخت و امروزه بسیاری از اکتشافت او بعنوان مهمترین قضایا در ریاضیات مطرح می باشند. زمینه های مورد علاقه او در ریاضیات بیشتر شامل نظریه اعداد، استفاده از هندسه تحلیلی در مقادیر بینهایت کوچک یا بزرگ و فعالیت در زمینه احتمالات بود.کارش در مورد مماسها الهام بخش نیوتن در طرح حساب دیفرانسیل و انتگرال شد.اصل مینیمم سازی فرما در اپتیک ،نتایج عمیقی در سراسر فیزیک بعد از او داشت.بالاتر از تمام اینها فرما به خاطر کارهایش در نظریه اعداد،در یادها مانده است.



از جمله قضایای زیبای او که به قضیه کوچک فرما معرف شده است می توان به این مورد اشاره کرد. اگر p یک عدد اول باشد و a یک عدد طبیعی در آنصورت بر p قابل قسمت خواهد بود.
اثبات این قضیه از طریق استقرای ریاضی بسیار ساده است. این قضیه حالت عمومی تر دو قضیه دیگر در ریاضیات هست یکی قضیه ای منسوب به اویلر (Euler) و دیگری قضیه ای معروف به همنهشتی چینی (Chinese Hypothesis).


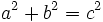از دیگر قضایایی که او در طول زندگی خود ارائه کرد می توان به موارد زیادی اشاره کرد از جمله : "اگر a و b و c اعداد صحیح باشند و باشد در آنصورت ab نمی تواند مربع یک عدد صحیح باشد." اولین بار برای این قضیه لاگرانژ (Lagrange) راه حلی استادانه ارائه کرد.
شاید جنجالی ترین قضیه ای که حتی خود فرما برای آن توضیح یا اثباتی ارائه نکرده است قضیه آخر او باشد که اینگونه است:

معادله در دامنه اعداد صحیح برای مقادیر بزگتر از 2 پاسخ ندارد.

این معادله ساده و فریبنده سالهای سال برای ریاضیدانان دردسر بزرگی بوده است چرا که فرما در حاشیه یکی از یادداشت های خود نوشته بود : "من برای این قضیه اثبات بسیار حیرت آوری (Marvelous) دارم." اما متاسفانه هرگز در میان نوشته های او اثبات این قضیه پیدا نشد و تاریخ همواره در شک و شبهه مانده است که آیا او این قضیه را اثبات کرده است یا خیر.
با وجود آنکه این قضیه تاکنون مورد علاقه بسیاری از ریاضی دانان بوده و بسیاری هم به ظاهر برای آن راه حل ارائه کرده اند اما بنظر می رسد هیچکدام از آنها استدلالهای کاملی نبوده و در نهایت این قضیه بنظر اثبات نشدنی می آید.